The dot product is a mathematical operation that takes two vectors and returns a scalar quantity. It is commonly used in various fields such as physics, engineering, and computer science to calculate the angle between two vectors or to project one vector onto another. Understanding how to take the dot product is essential for many mathematical applications.
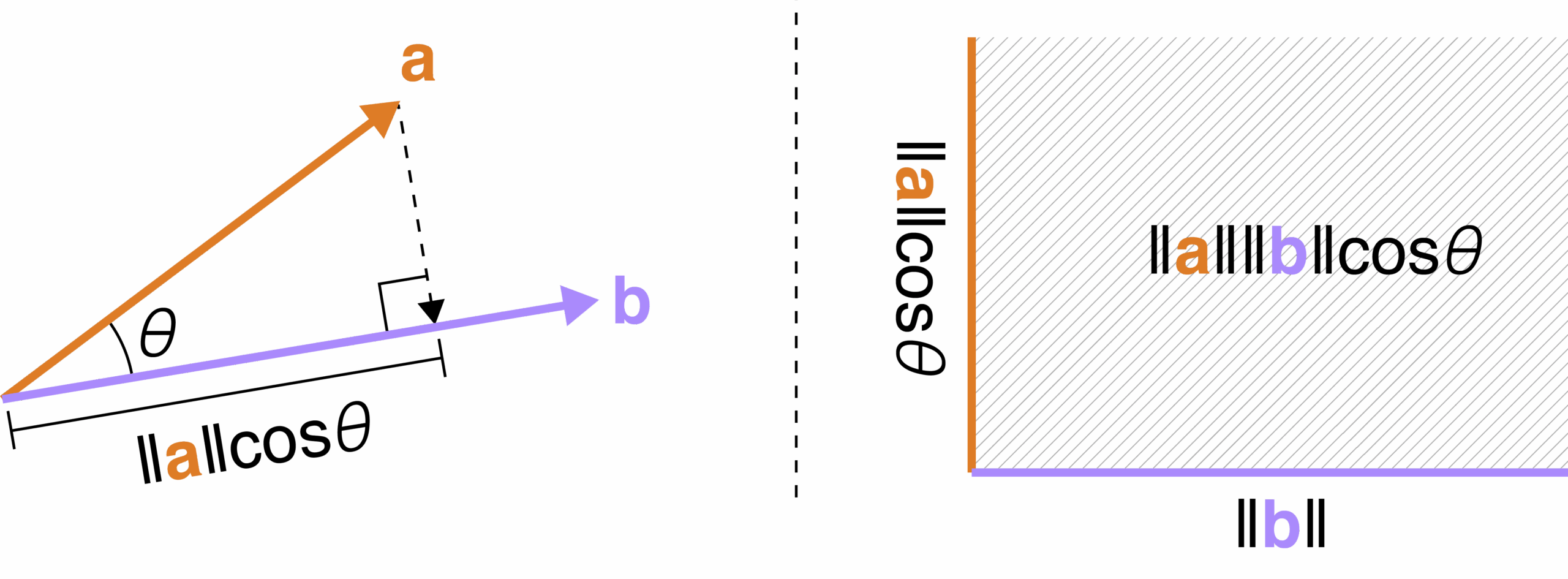
When taking the dot product of two vectors, it is important to remember that the result is a single number, not a vector. This number represents the cosine of the angle between the two vectors multiplied by the magnitudes of the vectors. The dot product is denoted by a dot (·) between the two vectors, such as A · B.
Steps to Take the Dot Product:
1. Multiply the corresponding components of the two vectors. For example, if you have vectors A = (a1, a2, a3) and B = (b1, b2, b3), the dot product A · B would be calculated as a1 * b1 + a2 * b2 + a3 * b3.
2. Sum up the results of the multiplications in step 1. This will give you the final scalar quantity that represents the dot product of the two vectors.
3. Alternatively, you can also calculate the dot product using the magnitudes of the vectors and the cosine of the angle between them. The formula for this method is A · B = |A| * |B| * cos(theta), where |A| and |B| are the magnitudes of vectors A and B, and theta is the angle between them.
4. The dot product can also be used to determine whether two vectors are orthogonal (perpendicular) to each other. If the dot product of two vectors is zero, then the vectors are orthogonal.
5. In programming languages such as Python or MATLAB, the dot product can be easily calculated using built-in functions or libraries. This can save time and effort when working with vectors and matrices in computational tasks.
Understanding how to take the dot product is essential for various mathematical and computational applications. By following the steps outlined above, you can efficiently calculate the dot product of two vectors and use this valuable operation in your work.